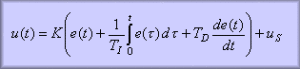A szakaszos technológiák általános jellemzői és a szabványok (elsősorban az S88.1. szabvány) bemutatása után a technológiairányítás egy lehetséges struktúráját tekintjük át, megalapozva ezzel az irányítási algoritmusok kapcsolatait is. Mindkét technológiatípus irányítása - már nem túlságosan összetett technológiáknál is - bonyolult mérnöki feladatot jelent, de a hierarchikus rendszerszemlélet eszközei és módszerei segítséget nyújtanak. Tekintsük a technológiairányítást egy olyan komplex algoritmusnak, amelynek a bemenetei a technológia mérőműszereinek jelei, kimenetei pedig a technológia beavatkozó szerveit működtető jelek. Az algoritmust fizikailag a folyamatirányító számítógépen realizáljuk.
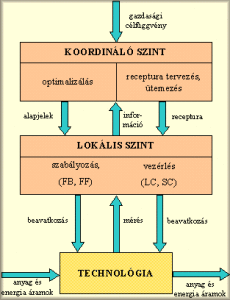
1. ábra: Az irányítási feladat strukturálása
Funkcionálisan két hierarchia szint értelmezhető (ld. 1. ábra):
- A technológiairányítás lokális szintje.
- A technológiairányítás koordináló szintje.
A lokális szint:
A lokális szintet az autonóm irányítási problémák sokasága adja, amelyekre a kis időléptékű változások a jellemzőek. A probléma megoldásban a néhány változót tartalmazó un. fekete doboz modelleket használjuk. A lokális szint többnyire önmagában is hierarchikus felépítésű (értéktartó szabályozások,kaszkád szabályozások, többváltozós szabályozások, stb.).
A folyamatos és szakaszos technológiák lokális szintű irányítási feladatainak egyik része teljes átfedésben van. Erre példák az alábbiak:
- Áramlás, hőmérséklet, nyomás, szint, stb. szabályozás,
- Logikai vezérlés, reteszelés, (személy-, készülék-, és környezetvédelem is),
- Számítási feladatok, pl. hőmérleg,
- Adatgyűjtés, dokumentálás.
A lokális irányítási feladatok egy másik jelentős része viszont csak a szakaszos rendszerekre jellemző. Ilyenek például az alábbiak:
- A szakaszos folyamat sorrendi vezérlése (bemérés, felfűtés, várakozás, hűtés, leürítés, stb.). Rugalmas logikai (LC) és sorrendi vezérlés (SC) a nagyszámú technológiai alternatíva, a váratlan helyzetek és üzemzavarok kezelésére.
- Több feldolgozó egységben folyó műveletek ütemezése és nyomon követése.
- Nyersanyagok betöltése a tartályokba, reaktorokba. Az egyes komponensek mennyiségeinek tömeg vagy térfogat alapján történő mérése.
- A technológiai jelek előírt vezetése (pl. felmelegítés, lehűtés, hőmérséklet tartás).
- Anyagok áttöltése a műveletek végén.
- A reakciók befejeződésének jelzése (analitikai mérés, hőmérséklet, viszkozitás).
- Batch naplók összeállítása (adagonként, műszakonként, naponta vagy hetente).
- Gyártás állapotának megjelenítése a kezelő számára, kezelői felület a recepturák, sorrendi és logikai vezérlések, szabályozások eléréséhez.
- A gyártáshoz szükséges összes információ kezelése.
A folyamatirányító rendszer funkcióit illetően a szakaszos rendszereknél lényegesen megnőtt a logikai feladatok mennyisége, de az analóg műveletek jelentősége sem csökkent. A változó termék ill. technológia következtében új igényként jelent meg a rugalmasság, amely átkonfigurálási lehetőséget jelent. A szakaszos jellegből következik, hogy az irányítás minőségi követelményeit tranziens állapotokra is ki kell terjeszteni. Hagyományos értelemben vett beállt állapot nincs is, így változó paraméterű rendszerekkel kell számolnunk, s ez különleges követelményeket támaszt a szabályozókkal szemben. Ezen problémák elsősorban adaptív vagy modellbázisú megoldásokkal kezelhetők. A rendszer tehát nem egy adott munkapont környezetében, hanem egy jelleggörbe mentén működik, s ezért annak nemlinearitása is kezelendő.
A koordináló szint:
A technológiairányítás koordináló szintje a teljes technológia egységét biztosítja. Formálisan egy nagy méretű, feltételes, szélsőérték-feladat megoldását igényli. A célfüggvény eredendően gazdasági, amely a teljes technológia működését minősíti, a feltétel pedig a teljes technológia matematikai modellje. A modellben az a priori (fehér doboz) jellegű rendszer elem modellek ill. hálózatok dominálnak. A feladat matematikai értelemben is nagy méretű, amelynek megoldásában a dekompozíció- koordináció elvét alkalmazhatjuk.
A vegyipari gyártás legfontosabb alapelemei:
- Az eljárás vagy receptura, amely a termék előállításának fizikai és kémiai műveleteit és annak részleteit határozza meg. - A vegyipari berendezések azon hálózata, amelyen a fizikai kémiai műveletek realizálhatók. - A piac, amely meghatározza a termékkel szembeni elvárásokat (mennyiség, minőség, stb.).
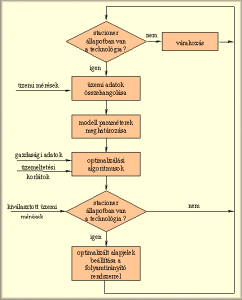
A folyamatosan működő technológiáknál a gépészetileg rögzített berendezéshálózat és a gyártási eljárás között időben állandó egy-egy értelmű kapcsolat áll fenn, amely a térbeli rögzítettség mellett egy időbeli állandóságot is eredményez. A technológia modellje emiatt többnyire stacioner jellegű. A folyamatos technológiák on-line optimalizálásának sémáját a 2. ábra szemlélteti:
2. ábra: A folyamatos technológiák optimalizálása
Szakaszos rendszereknél a receptura és a gépészetileg rögzített berendezéshálózat egymáshoz rendelése több-több értelmű, amely a szakaszos rendszerek rugalmasságát eredményezi: többtermékes (multiproduct) gyártás, többcélú üzem (multipurpose plant), stb. Ez azt eredményezi, hogy szakaszos technológiáknál a koordináló irányítás lényegesen különbözik a folyamatos technológiáknál bemutatottól. Az online optimalizálással szemben itt a receptura tervezés ill. az ütemezés játssza a főszerepet.
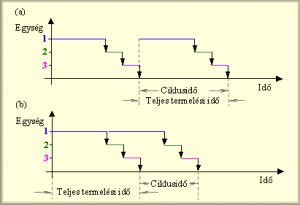
Az ütemezési feladatban a receptura, a készülékek és a hozzájuk rendelendő műveletek ismertek. Feladat a megfelelő hozzárendelések meghatározása. A 3. ábra egy 3 berendezést felhasználó gyártás nem-átfedő (a) ill. átfedő (b) ütemezését illusztrálja. Az a. részen a 2. gyártást az 1. gyártás befejezése után indítjuk, amíg a b. részen jól látható, hogy az 1. berendezés szabaddá válása után indítjuk a 2. gyártást, s ezzel a technológia kapacitását megnöveltük. Az ideális eset az lenne, ha minden berendezés állandóan és teljes kapacitással üzemelne!
3. ábra: Nem átfedő és átfedő ütemezés
A kapacitást meghatározó ciklusidő csökkentésére különböző lehetőségeink vannak:
- Párhuzamos, időben eltolt fázisban üzemelő berendezések.
- Feladatok összevonása és szétválasztása.
- Közbülső tárolók alkalmazása.
- Különböző feladatfolytatások alkalmazása.
Az ütemezés ugyancsak egy nagyméretű matematikai probléma, amely megoldásához az egész értékű programozást használhatjuk. A korszerű folyamatirányító berendezések egyre inkább lehetővé teszik a felvázolt, különböző szintű algoritmusok realizálását.
Ebben a részben a lokális szintű szabályozóalgoritmusokat tekintjük át, a szakaszos rendszerek igényeit figyelembe véve. A szabályozótervezés a megfelelő irányítási algoritmus kiválasztását és a benne szereplő paraméterek meghatározását (hangolás) foglalja magába. A modellbázisú (elsősorban predikciós) szabályozók mintegy két évtizedes ipari alkalmazása és a megalapozásukat szolgáló intenzív akadémiai kutatások ellenére is a visszacsatolt struktúrában használt PI ill. PID alapú szabályozók uralják a vegyipari technológiákat. A dominancia legfontosabb okai a PID szabályozók klasszikus technikában betöltött szerepe, az oktatásban elfoglalt helye, a DCS rendszerekben való kiépítettsége és nem utolsósorban valós alkalmazásuk hatékonysága. Ráadásul más modellbázisú technikák, az objektum modelljétől függően, gyakran PID algoritmust eredményeznek, s ezáltal PID szabályozóként installálhatók. Mindezek ellenére a modellalapú szabályozóalgoritmusok kutatását és alkalmazását is fontosnak tartjuk, elsősorban olyan objektumoknál, amelyeknél a PID alkalmazása kevésbé hatékony. A modellbázisú algoritmusok vizsgálata a technikai lehetőségek bővülésével egyre intenzívebb, az analízisben egyre nagyobb szerepet kap a vizsgált technológia modellje.
PID alapú batch algoritmusok
Az alap PID algoritmus inputja a hibajel (e), outputja pedig a beavatkozó jel (u), folytonos időtartománybeli modellje az alábbi:
ahol K, Ti, Td a PID paraméterek (erősítési tényező, integrálási ill. differenciálási időállandók), uspedig a stacioner beavatkozó jel.
A folyamatirányító rendszerekben a PID különböző modifikációit realizálják. Szakaszos rendszereknél lehetőség van us pontosabb becslésére: us=u0+FF(w,z,K)
ahol u0 konstans (a szakaszos rendszer különböző fázisaiban iniciálásra használható), FF pesig az alapjeltől (w) és a mért zavarás(ok)tól (z,K) függő előrecsatolás.
Korábban kihangsúlyoztuk, hogy a szakaszos rendszerek teljes működésük során állandóan tranziens állapotban vannak (változó munkapont), a PID szabályozók beállítása viszont csak egyetlen munkapontra optimális. Ez az ellentmondás az adaptív sémákban oldható fel. Szakaszos rendszerekben leggyakrabban a programozott adaptációs megoldást használjuk. Ennek az a lényege, hogy a recepturát ismerve, az alkalmazandó PID paramétereket az idő(vagy más kisegítő változó) függvényében előre beprogramozzuk.
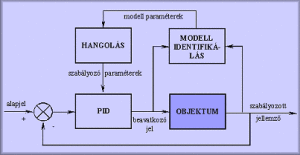
Mind a szakaszos mind a folyamatos technológiákban elterjedtek az önhangoló adaptív szabályozók ( ld. alábbi ábra: )
Ezen típusnak az a lényege, hogy egy feltételezett objektum modell alapján (leggyakrabban elsőrendű holtidős szakasz) on-line identifikációt végzünk, amely a megfelelő modell paramétereket szolgáltatja. Az ilyen értelemben pontosított modell alapján egy hangolási módszerrel meghatározzuk a szabályozó algoritmus aktuális paramétereit. Szakaszos rendszerek identifikációjánál az un. felejtési tényezővel vehető figyelembe a munkapont változása.
Modellbázisú szabályozó algoritmusok
A visszacsatoláson alapuló szabályozások alapproblémája az, hogy a pillanatnyi beavatkozás hatása a kimeneten - különösen holtidős, magasabb rendű rendszereknél - időben késleltetve jelentkezik. A kimenet kis változása nagyobb beavatkozásra késztet, ami végső soron instabilitáshoz is vezethet. Az objektum matematikai modelljének megismerése lehetőséget ad egy beavatkozás jövőbeli hatásának becslésére, s az optimális beavatkozás meghatározására. Az MPC (Modell Predictive Controller) szabályozók ipari alkalmazásának több mint két évtizedes múltja van, s terjednek azok a szoftverek is (pl. RMPCT), amelyek a tervezést nagymértékben segítik. Elsősorban többváltozós (MIMO) problémákra, PID körökre szuperponálva alkalmazhatóak gazdaságosan. Egyszerű SISO feladatoknál ugyanis az MPC teljesítőképessége a PID-éhez mérhető, a számításigénye és installációs ára viszont lényegesen magasabb lehet.
A legegyszerűbb modellbázisú tervezési módszerek egyike a közvetlen szintézis módszer. Ennek alapötlete az, hogy először definiáljuk a zártköri dinamikát, majd az objektum modelljének ismeretében visszaszámoljuk hogy ennek kézben tartására milyen paraméterekkel rendelkező szabályozó szükséges.
A tervezési alapegyenlet az alábbi: Gc=1/Gs * Gw / (1-Gw) , ahol Gc kívánatos szabályozó átviteli függvénye, Gs a szabályozandó objektum átviteli függvénye, Gw a zárt kör specifikált átviteli függvénye.
Egyszerűbb objektumok esetén gyakran PID variánst kapunk eredményként, amely bármely DCS rendszeren könnyen installálható. A zárt kört elsőrendű, holtidős tagként (HPT1) definiálva, néhány egyszerűbb objektumra a közvetlen szintézis módszerrel való tervezés eredményét az alábbi táblázatban adjuk meg:
| Objektum modell | K * Kc | Ti | Td |
| K / Ts+1 | T / Tc | T | 0 |
| K / (T1s+1)(T2s+1) | (T1+T2) / Tc | T1 + T2 | (T1 * T2)(T1 + T2) |
| K / s | 1 / Tc | végtelen | 0 |
| K * e-Th s / T s+1 | T / (Tc + Th) | T | 0 |
| K / (s * (Ts+1)) | 1 / Tc | végtelen | T |
Az Internal Modell Controller
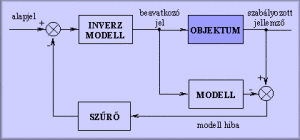
Az akadémiai vizsgálatokban népszerű IMC (Internal Modell Controller) szabályozó lényege az objektum inverz modelljére épülő előrecsatolás, amelynél a modell hibájából adódó maradó szabályozási eltérést a szűrt modellhiba visszacsatolásával korrigáljuk (ld. alábbi ábránk:).
Az objektum modelljének függvényében itt is gyakran adódik klasszikus visszacsatolt struktúrába beírható PID algoritmus. (Az 1. táblázatbeli objektumokra IMC szabályozó tervezéssel is a táblázatbeli eredményeket kapjuk, ha elsőrendű szűrőket alkalmazunk.)
A modellbázisú algoritmusok alkalmazásánál fontos szerepet játszik az irányítandó objektum adekvát modelljének elkészítése. A modellezéshez a legkülönbözőbb modell típusokból választhatunk. Leggyakrabban fekete doboz modellekkel dolgozunk, mint például a klasszikus bemenet-kimenet modell (Laplace- ill. z-transzformált tartományban átviteli függvény), vagy egyre gyakrabban állapottér modell, neurális hálózati modell, stb. Mindezek determinisztikus ill. sztochasztikus verziói mellett a fuzzy modellek alkalmazásával is egyre sűrűbben találkozunk. Az iparilag alkalmazott MPC algoritmusokban például leggyakrabban a kísérletileg könnyen meghatározható súly- ill. átmeneti függvényeken alapuló konvolúciós modelleket használják. Emiatt szakaszos rendszerekben az MPC nehezebben alkalmazható.
Szakaszos rendszerek irányításához is jó keretet biztosít viszont az IMC struktúra , amelyben a legkülönbözőbb modelltípusok is viszonylag könnyen realizálhatók. Neurális hálózati modell esetén például még az invertálás nehézsége is megkerülhető - amennyiben az inverz modellt nem a modell invertálásával állítjuk elő - hanem azt az inverz feladatra betanított neurális hálózati modell helyettesíti. A modellbázisú algoritmusokban a valóság és a modell eltérését a modellhiba visszacsatolásával vehetjük figyelembe. Ezen algoritmusoknál is lehetőség van a már említett adaptív struktúrák alkalmazására. Sőt batch rendszereknél egy újabb lehetőség is kínálkozik a javításra: Azonos vagy hasonló recepturák szerinti gyártásoknál a megelőző gyártás(ok) tapasztalatai az új gyártásnál felhasználhatók (tanuló szabályozás).
A szakaszos rendszerek irányításával szemben megkövetelt minőségi ígények egyre inkább megkövetelik a klasszikus PID-szabályozókon túlmutató modell bázisú algoritmusok alkalmazását, s ezzel párhuzamosan a folyamatirányító berendezések egyre inkább nyitottá válnak az ilyen algoritmusok installálására.
A következő (záró) részben a validálás kérdéskörét mutatjuk be.